Definition Of An Arithmetic Sequence

Arithmetic Sequence

The arithmetic sequence is the sequence where the common departure remains abiding between whatever two successive terms. Let united states of america recall what is a sequence. A sequence is a collection of numbers that follow a pattern. For example, the sequence 1, 6, 11, 16, … is an arithmetic sequence because there is a pattern where each number is obtained by calculation 5 to its previous term. We take two arithmetic sequence formulas.

• The formula for finding north^th term of an arithmetic sequence
• The formula to find the sum of first north terms of an arithmetics sequence

If nosotros want to observe any term in the arithmetic sequence then we can employ the arithmetic sequence formula. Let us learn the definition of an arithmetics sequence and arithmetic sequence formulas forth with derivations and a lot more examples for a meliorate understanding.

1.	What is an Arithmetic Sequence?
2.	Arithmetic Sequence Formula
3.	Nth Term of Arithmetic Sequence
4.	Sum of Arithmetics Sequence
v.	Deviation Between Arithmetics Sequence and Geometric Sequence
half-dozen.	FAQs on Arithmetics Sequence

What is an Arithmetic Sequence?

An arithmetics sequence is defined in two means. It is a "sequence where the differences between every two successive terms are the same" (or) In an arithmetics sequence, "every term is obtained past calculation a fixed number (positive or negative or nothing) to its previous term". The following is an arithmetics sequence as every term is obtained by adding a fixed number 4 to its previous term.

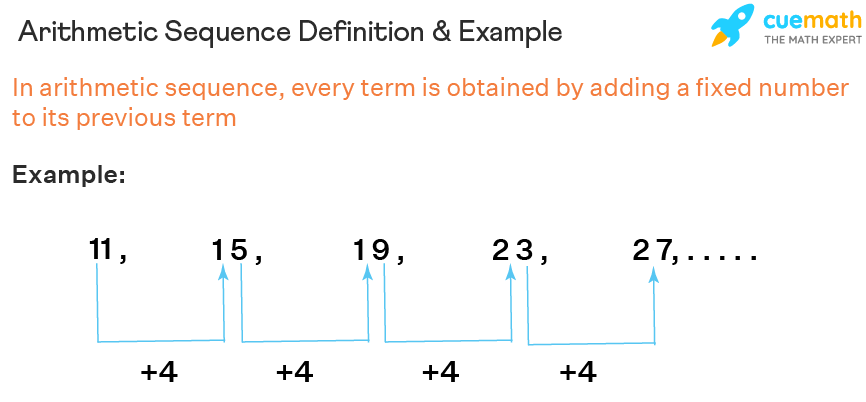
Arithmetic Sequence Example

Consider the sequence three, 6, 9, 12, fifteen, .... is an arithmetic sequence because every term is obtained by calculation a constant number (3) to its previous term.

Here,

• The first term, a = 3
• The common difference, d = 6 - iii = ix - half-dozen = 12 - nine = xv - 12 = ... = iii

Thus, an arithmetic sequence can exist written as a, a + d, a + second, a + 3d, .... Let the states verify this pattern for the above example.

a, a + d, a + 2d, a + 3d, a + 4d, ... = 3, 3 + three, 3 + 2(3), 3 + 3(3), 3 + four(three),... = 3, 6, 9, 12,xv,....

A few more than examples of an arithmetic sequence are:

• 5, 8, 11, fourteen, ...
• 80, 75, 70, 65, 60, ...
• π/two, π, 3π/2, 2π, ....
• -√two, -2√2, -3√two, -4√2, ...

Arithmetics Sequence Formula

The first term of an arithmetic sequence is a, its mutual difference is d, due north is the number of terms. The general form of the AP is a, a+d, a+second, a+3d,......up to n terms. We have dissimilar formulas associated with an arithmetics sequence used to summate the northward^th term, the sum of north terms of an AP, or the common difference of a given arithmetic sequence.

The arithmetic sequence formula is given as,

• Northward^thursday Term: a_north = a + (northward-one)d
• S_n = (n/2) [2a + (n - 1)d]
• d = a_n - a_n-1

Nth Term of Arithmetic Sequence

The northward^th term of an arithmetic sequence a₁, a_ii, a_iii, ... is given by a_northward = a _ane + (north - ane) d. This is also known as the general term of the arithmetic sequence. This directly follows from the understanding that the arithmetic sequence a₁, a₂, a₃, ... = a₁, a₁ + d, a_i + 2d, a₁ + 3d,... The following table shows some arithmetic sequences along with the showtime term, the common difference, and the n^th term.

Arithmetics Sequence	First Term (a)	Common Difference (d)	nth term adue north = a one + (north - ane) d
80, 75, 70, 65, lx, ...	80	-5	80 + (n - 1) (-five) = -5n + 85
π/ii, π, 3π/2, 2π, ....	π/2	π/2	π/2 + (n - 1) (π/2) = nπ/2
-√ii, -2√2, -3√2, -iv√2, ...	-√2	-√2	-√2 + (due north - 1) (-√ii) = -√two n

Arithmetic Sequence Recursive Formula

The above formula for finding the n^{t h} term of an arithmetic sequence is used to notice any term of the sequence when the values of 'a₁' and 'd' are known. In that location is another formula to find the n^th term which is chosen the "recursive formula of an arithmetic sequence" and is used to find a term (a_n) of the sequence when its previous term (a_n-ane) and 'd' are known. It says

a_n = a_n-1 + d

This formula just follows the definition of the arithmetic sequence.

Case: Discover a₂₁ of an arithmetic sequence if a_nineteen = -72 and d = vii.

Solution:

By using the recursive formula,

a_xx = a₁₉ + d = -72 + 7 = -65

a₂₁ = a_xx + d = -65 + vii = -58

Therefore, a₂₁ = -58.

Arithmetics Series

The sum of the arithmetic sequence formula is used to find the sum of its first northward terms. Annotation that the sum of terms of an arithmetic sequence is known equally arithmetic serial. Consider an arithmetics series in which the starting time term is a₁ (or 'a') and the common difference is d. The sum of its first n terms is denoted by South_n. Then

• When the n^th term is NOT known: S_n= n/two [2a₁ + (due north-i) d]
• When the n^th term is known: Due south_n = northward/ii [a₁ + a_north]

Instance

Ms. Natalie earns $200,000 per annum and her salary increases by $25,000 per annum. And then how much does she earn at the end of the first 5 years?

Solution:

The amount earned past Ms. Natalie for the first year is, a = 2,00,000. The increment per annum is, d = 25,000. We have to calculate her earnings in the get-go 5 years. Hence n = 5. Substituting these values in the sum sum of arithmetics sequence formula,

South_{due north}= n/two [2a₁ + (n-1) d]

⇒ S_northward = 5/two(2(200000) + (5 - 1)(25000))

= 5/ii (400000 +100000)

= 5/2 (500000)

= 1250000

She earns $1,250,000 in 5 years. We can utilise this formula to be more than helpful for larger values of 'due north'.

Sum of Arithmetics Sequence

Permit us take an arithmetic sequence that has its beginning term to be a₁ and the common difference to be d. Then the sum of the showtime 'due north' terms of the sequence is given by

South_{due north} = a₁ + (a₁ + d) + (a_one + 2d) + … + a_{due north} ... (1)

Permit us write the aforementioned sum from right to left (i.e., from the due north^th term to the beginning term).

S_n = a_n + (a_{due north} – d) + (a_n – 2d) + … + a₁ ... (2)

Adding (one) and (2), all terms with 'd' get canceled.

2S_n = (a_ane + a_north) + (a₁ + a_n) + (a_one + a_n) + … + (a_i + a_n)

2S_n = n (a₁ + a_n)

S_{due north} = [north(a_one + a_n)]/2

By substituting a_n = a₁ + (due north – 1)d into the last formula, we accept

S_n = northward/2 [a_ane + a_one + (n – ane)d] (or)

S_n = n/2 [2a_i + (n – one)d]

Thus, we have derived both formulas for the sum of the arithmetic sequence.

Difference Between Arithmetic Sequence and Geometric Sequence

Hither are the differences betwixt arithmetic and geometric sequence:

Arithmetic Sequence	Geometric Sequence
In this, the differences between every ii consecutive numbers are the same.	In this, the ratios of every two consecutive numbers are the same.
It is identified by the first term (a) and the common difference (d).	It is identified by the first term (a) and the common ratio (r).
There is a linear human relationship betwixt the terms.	There is an exponential human relationship between the terms.

Important Notes on Arithmetic Sequence:

• In arithmetic sequences, the deviation between every ii successive numbers is the same.
• The common difference of an arithmetic sequence a_i, a_ii, a_three, ... is, d = a₂ - a₁ = a₃ - a_ii = ...
• The n^th term of an arithmetic sequence is a_northward = a_one + (north−1)d.
• The sum of the first n terms of an arithmetics sequence is S_n = northward/2[2a₁ + (n − i)d].
• The common difference between arithmetic sequences can exist either positive or negative or nil.

☛ Related Topics:

• Sequence Calculator
• Series Calculator
• Arithmetic Sequence Calculator
• Geometric Sequence Calculator

Arithmetic Sequence Examples

1. Case i: Find the n^th term of the arithmetic sequence -5, -7/2, -2, ....

   Solution:

   The given sequence is -5, -7/2, -two, ...

   Hither, the first term is a = -5, and the common difference is, d = -(7/two) - (-5) = -ii - (-7/2) = ... = 3/two.

   The due north^th term of an arithmetic sequence is given past

   a_n = a₁ + (north−1)d

   a_north = -5 +(n - 1) (iii/ii)

   = -5+ (3/ii)n - 3/2

   = 3n/2 - 13/2

   Answer: The n^th term of the given arithmetic sequence is, a_north = 3n/two - 13/2.

2. Case 2: Which term of the arithmetic sequence -3, -8, -13, -18,... is -248?

   Solution:

   The given arithmetic sequence is -3, -eight, -13, -xviii,...

   The first term is, a = -3

   The common difference is, d = -8 - (-three) = -13 - (-8) = ... = -5.

   Information technology is given that the n^th term is, a_north = -248.

   Substitute all these values in the n^th term of an arithmetic sequence formula,

   a_n = a_ane + (northward−1)d
   ⇒ -248 = -three + (-5)(north - 1)
   ⇒ -248 = -3 -5n + v
   ⇒ -248 = 2 - 5n
   ⇒ -250 = -5n
   ⇒ n = 50

   Answer: -248 is the l^th term of the given sequence.

3. Instance 3: Find the sum of the arithmetic sequence -iii, -8, -13, -eighteen,.., -248.

   Solution:

   This sequence is the same as the one that is given in Example 2.

   In that location we found that a = -iii, d = -v, and due north = l.

   So nosotros take to find the sum of the 50 terms of the given arithmetic serial.

   S_n = n/2[a₁ + a_n]

   S₅₀ = [50 (-three - 248)]/2 = -6275

   Respond: The sum of the given arithmetic sequence is -6275.

become to slidego to slidego to slide

Have questions on basic mathematical concepts?

Get a problem-solving gnaw using logic, not rules. Learn the why behind math with our certified experts

Book a Free Trial Class

Arithmetic Sequence Questions

get to slidego to slide

FAQs on Arithmetic Sequence

What is an Arithmetic Sequence in Algebra?

An arithmetic sequence in algebra is a sequence of numbers where the difference between every two sequent terms is the same. Generally, the arithmetic sequence is written as a, a+d, a+2d, a+3d, ..., where a is the first term and d is the mutual difference.

What are Arithmetic Sequence Formulas?

Here are the formulas related to an arithmetics sequence where a₁ (or a) is the offset term and d is a common difference:

• The common deviation, d = a_n - a_n-1.
• northward^thursday term of sequence is, a_n = a + (north - 1)d
• Sum of n terms of sequence is , South_n = [n(a_ane + a_n)]/2 (or) due north/2 (2a + (n - 1)d)

What is the Definition of an Arithmetics Sequence?

A sequence of numbers in which every term (except the first term) is obtained by adding a constant number to the previous term is chosen an arithmetic sequence. For case, 1, 3, 5, 7, ... is an arithmetic sequence every bit every term is obtained past adding two (a constant number) to its previous term.

How to Place An Arithmetic Sequence?

If the deviation between every ii consecutive terms of a sequence is the same then it is an arithmetic sequence. For example, 3, 8, xiii, xviii ... is arithmetic because the sequent terms have a fixed divergence.

• 8-iii = v
• 13-8 = five
• 18-13 = 5 and then on.

What is the north^th term of an Arithmetics Sequence?

The n^th term of arithmetic sequences is given by a_northward = a + (northward – 1) × d. Here 'a' represents the outset term and 'd' represents the common divergence.

What is an Arithmetic Series?

An arithmetic series is a sum of an arithmetic sequence where each term is obtained by adding a stock-still number to each previous term.

What is the Arithmetic Series Formula?

The sum of the first north terms of an arithmetic sequence (arithmetic series) with the first term 'a' and common deviation 'd' is denoted by Sₙ and we accept two formulas to find it.

• Southward_{due north} = northward/ii[2a + (northward - 1)d]
• Due south_n = n/2[a + a_northward].

What is the Formula to Notice the Mutual Divergence in Arithmetics sequence?

The common difference of an arithmetics sequence, as its proper noun suggests, is the difference between every two of its successive (or consecutive) terms. The formula for finding the mutual difference of an arithmetic sequence is, d = a_n - a_n-one.

How to Detect n in Arithmetics Sequence?

When nosotros have to find the number of terms (due north) in arithmetic sequences, some of the information most a, d, a_n or S_n might take been given in the problem. We will simply substitute the given values in the formulas of a_{due north} or S_n and solve it for north.

How To Find the Offset Term in Arithmetics sequence?

The commencement term of an arithmetic sequence is the number that occurs in the first position from the left. Information technology is denoted by 'a'. If 'a' is Not given in the trouble, then some information most d (or) a_n (or) Southward_n might be given in the problem. We volition just substitute the given values in the formulas of a_{due north} or S_n and solve it for 'a'.

What is the Divergence Between Arithmetic Sequence and Arithmetic Serial?

An arithmetic sequence is a collection of numbers in which all the differences betwixt every two sequent numbers are equal to a constant whereas an arithmetic series is the sum of a few or more than terms of an arithmetic sequence.

What are the Types of Sequences?

In that location are mainly 3 types of sequences in math. They are:

• Arithmetic sequence
• Geometric sequence
• Harmonic sequence

What are the Applications of Arithmetics Sequence?

Here are some applications: the bacon of a person which is increased by a constant amount by each year, the rent of a taxi which charges per mile, the number of fishes in a pond that increment by a constant number each month, etc.

How to Detect the n^th Term in Arithmetic Sequence?

Here are the steps for finding the northward^thursday term of arithmetic sequences:

• Identify its kickoff term, a
• Common divergence, d
• Identify which term you want. i.e., n
• Substitute all these into the formula a_{due north} = a + (n – one) × d.

How to Find the Sum of n Terms of Arithmetic Sequence?

To find the sum of the first n terms of arithmetics sequences,

• Place its beginning term (a)
• Common deviation (d)
• Place which term y'all desire (north)
• Substitute all these into the formula S_n= (due north/2)(2a + (n - 1)d)

Definition Of An Arithmetic Sequence,

Source: https://www.cuemath.com/algebra/arithmetic-sequence/

Posted by: helmdoughs.blogspot.com

Share this post