Area Of A Trapezoidal Prism

Area of a trapezoid

The area of a trapezoid is the space independent within its perimeter. The grey space is the expanse of the trapezoid in the diagram below.

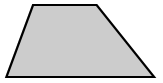
Expanse formula of a trapezoid

The area, A, of a trapezoid is:

where h is the height and b₁ and b₂ are the base lengths.

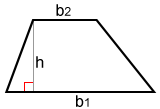
Derivation

Given a trapezoid, if we class a coinciding trapezoid and rotate it such that the 2 congruent trapezoids can be joined together to form a parallelogram equally shown by the congruent blackness and gray trapezoids below.

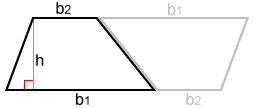
The surface area of a parallelogram is A = bh. The parallelogram formed by the two coinciding trapezoids has a base b_one + b₂ and height h. Therefore, the expanse of this parallelogram is: A = (b_ane + b₂)h. Since the parallelogram is made up of two coinciding trapezoids, halving the above formula gives u.s.a. the formula for the area of one of the trapezoids:

Example:

Find the area of a trapezoid that has summit of 16 and bases of 18 and 35.

Plugging these into the area formula:

Using the midsegment

The midsegment of a trapezoid is a line segment connecting the midpoint of its legs. A midsegment has a length that is the average of its ii bases, which is

The area, A, of a trapezoid using the length of the midsegment is:

A = hm

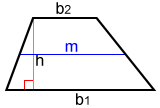
Derivation

Substituting the value for m into the original trapezoid area formula:

Finding area using a grid

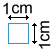
Another way to find the area of a trapezoid is to determine how many unit squares it takes to cover its surface. Below is a unit square with side lengths of 1 cm.

A grid of unit squares can be used when determining the expanse of a trapezoid.

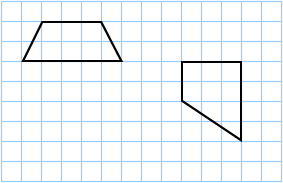
The grid higher up contains unit of measurement squares that have an area of i cm² each. The trapezoid on the left contains 6 full squares and 4 partial squares, so it has an surface area of approximately:

The trapezoid to the right contains seven full squares and iv partial squares, and so it has an surface area of approximately:

This method can be used to find the expanse of any shape; it is not limited to trapezoids. However, it is only an gauge value of the area. The smaller the unit square used, the higher the accuracy of the approximation. Using a grid fabricated upward of ane mm squares is 10 times more accurate than using a grid made up of 1 cm squares.